現在退出會丟失進度,確定嗎
債券和債務管理
課前準備
良好的債務結構可以爲企業拓寬融資管道,有利於企業的發展。但是,鉅額負債也會直接壓垮整個企業。今天,讓我們來認識債券,學習其收益的計算方法。
單選題
債券的種類有很多,下列中風險最小,安全性最好的是?
根據發行方的不同,債券可分爲政府債券、金融債券以及公司債券。投資者購買了債券,就如同將資金借予政府、大企業或其他債券發行機構。這三者中,政府債券因爲有政府稅收作爲保障,因而風險最小,但收益也最小。公司債券風險最大,可能的收益也最大。
- 政府債券
- 金融債券
- 公司債券
- 企業債券
判斷題
請判斷下列關於債券特徵的說法是否正確。
正確
錯誤
正確,此爲債券特徵的償還性。
債券一般會規定償還期限,發行人須按約定條件償還本金並支付利息。
錯誤,債券具有流通性。
債券不可以在流通市場上進行自由轉讓。
正確,此爲債券的安全性。
與股票相比,債券通常規定有固定的利率。與企業績效沒有直接聯繫,收益比較穩定,風險較小。
正確,債券具有收益性。除了利息收入,投資者還可以利用債券的價格變動,買賣賺取差額。
投資債券可以給投資者定期或不定期地帶來利息收入。
單選題
債券的風險性和盈利性緊密相連,主要表現在
浮動利率債券的息票率是隨市場利率變動而調整的利率,是同當前市場掛鉤的。投資債券依舊存在風險,只是較之其他投資行爲,風險較小。
- 債券的利率和風險都是規定好的,不可變更的。
- 債券利率高低同債券本身的風險成正比。
- 債券的利率高低與發行人的信譽成正比。
- 購買債券作爲投資行爲沒有風險。
單選題
投資債券的最好環境是?
在穩定的低通貨膨脹的情況下,很難出現嚴重的通貨膨脹和利率的大幅上升,這樣就會使債券市場具有長期投資價值。
- 穩定的高通貨膨脹率
- 穩定的低通貨膨脹率
- 兩者皆可
- 兩者皆不可。
單選題
浮動利率票據也可以被稱爲?
正確。浮動利率票據(Floating Rate Notes,FRNs)又稱浮動利率債券,是票面利率在票據的存續期間內會變動,而非固定不變,浮動的方式可由契約雙方約定,其票面利率部分可連接不同的參考利率或者不同的利率衍生產品。
- 零息債券
- 指數掛鉤債券
- 固定利率債券
- 可變利率債券
單選題
債券的利率敏感程度與哪些因素相關?
正確。
- 收益率
- 息票利息
- 到期年限
- 以上所有
債券的價值評估
對債券的價值評估是非常重要的,主要基於以下兩個原因:(移動滑鼠檢視詳情)
- 原因之一
- 在開始設定合同條款的過程中,合同方需要擁有一項得到一致同意的價值評估流程。
- 原因之二
- 固定收益證券經常在它們到期之前被出售,因爲決定其價值的市場因素——利率隨時間推移而發生變化,所以賣方和買方都不得不在每次交易的時候重新對它們進行價值評估。
有關債券價值與收益的計算方法
瞭解了債券價值的評估的重要性後,我們來看一下如何具體的計算債券的價值與收益率。
下面將會出現幾個計算公式,請牢記它們,後面會有相應的計算題,檢驗自己是否理解了公式。
通常情況下,我們將情況分爲三種(移動滑鼠檢視詳情)
下面將會出現幾個計算公式,請牢記它們,後面會有相應的計算題,檢驗自己是否理解了公式。
通常情況下,我們將情況分爲三種(移動滑鼠檢視詳情)
- 基本的價值評估模型
- 用擁有單一折現率的折現現金流計算公式估計承諾的未來現金流價值。
利率爲i,n期內每期定期繳款數額爲PMT美元的普通年金計算公式: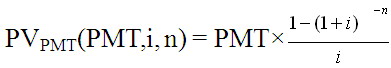 。
。
利率爲i,n爲期限,每期定期繳款數額爲PMT美元
例:你購買一隻承諾在接下來的3年中每年支付100美元的固定收益證券,折現率每年6%,年金價值=100×(1-(1+6%)^-3)/6%=267.30美元
- 用擁有單一折現率的折現現金流計算公式估計承諾的未來現金流價值。
- 純粹折現債券的收益率
- 純粹折現債券是對所有承諾已知現金流的合同進行價值評估的基本構成要素。其收益率是購買該債券並將其持有至到期的投資者的年度化收益率。1年期純粹折現債券的收益率=(面值-價格)/價格.然而如果該債券擁有不同於1年的到期期限,那麼我們將使用限值公式得出它的年收益率:
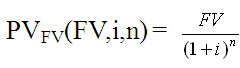
例:一隻面值爲1000美元且價格爲880美元的2年期純粹折現債券,其收益率=6.60%
- 純粹折現債券是對所有承諾已知現金流的合同進行價值評估的基本構成要素。其收益率是購買該債券並將其持有至到期的投資者的年度化收益率。1年期純粹折現債券的收益率=(面值-價格)/價格.然而如果該債券擁有不同於1年的到期期限,那麼我們將使用限值公式得出它的年收益率:
- 真實世界中債券的主要特徵
- 這一項我們會在稍後進行詳細講解。
變化中的總現值計算
請回想上一頁中,3年裏每年支付100美元的證券的價值評估過程。而實際生活中,我們觀測到了純粹折現債券的變化的價格集合(如下表)
由此得出,總現值爲:
第一年現金流的現值=100/1.0526=95.00美元
第2年現金流的現值=100/1.0660^2=88.00美元
第3年的現金流的現值=100/1.0772^3=80.00美元
總現值=263美元
| 到期期限 | 按1美元面值報出的價格 | 收益率(每年) |
|---|---|---|
| 1年 | 0.95 | 5.26% |
| 2年 | 0.88 | 6.60% |
| 3年 | 0.80 | 7.72% |
由此得出,總現值爲:
第一年現金流的現值=100/1.0526=95.00美元
第2年現金流的現值=100/1.0660^2=88.00美元
第3年的現金流的現值=100/1.0772^3=80.00美元
總現值=263美元
變化中的總現值計算
那麼在上一種情況中,是否存在單一的折現率呢?答案是存在單一折現率,計算公式爲:
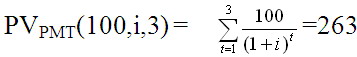
由此得出,單一折現率爲6.88%
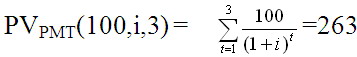
| n | i | PV | FV | PMT | 結果 |
|---|---|---|---|---|---|
| 3 | ? | -263 | 0 | 100美元 | i=6.88% |
由此得出,單一折現率爲6.88%
計算題
假定你購買了承諾每年支付100美元的3年期的固定收益債券,而其市場利率從6%降至每年5%,請問它的價值將會發生什麼變化?
正確。公式請參考前面一頁的普通年金計算公式:市場利率爲6%時,價值爲267.30美元;利率降至5%時,價值升至272.32美元。
由此,我們也可以發現一個基本原理——市場利率的變化將導致所有現存承諾未來固定支付的合同的市場價值反向變動。
由此,我們也可以發現一個基本原理——市場利率的變化將導致所有現存承諾未來固定支付的合同的市場價值反向變動。
- 從267.30美元上升至272.32美元
- 從267.30美元下降至262.43美元
- 從262.43美元上升至272.32美元
- 從262.43美元上升至267.30美元
計算題
如表,計算每年支付100美元的3年期年金價值爲多少?單一折現率呢?
| 到期期限 | 按1美元面值報出的價格 | 收益率(每年) |
|---|---|---|
| 1年 | 0.95 | 5.26% |
| 2年 | 0.88 | 6.00% |
| 3年 | 0.80 | 7.72% |
正確。
- 267美元,6.67%
- 267美元,4.89%
- 264美元,6.67%
- 264美元,4.89%
單選題
如果收益率下降,債券的價格將會?
正確
- 上漲
- 下跌
- 不變
- 不定
附息債券以及其收益率的計算方法
附息債券要求發行者在債券存續期間對債券持有者進行利息的定期支付——稱爲息票支付,然後在債券到期時支付債券的面值。
而當附息債券的價格不同於其面值的時候,收益率這一術語的意思本身就會變得含糊不清。
同時,我們也有兩種不同的收益率計算方法,第一種稱爲當期收益率,第二種稱爲到期收益率
下面我們主要分爲以下三種情況討論:(移動滑鼠檢視詳情)
而當附息債券的價格不同於其面值的時候,收益率這一術語的意思本身就會變得含糊不清。
同時,我們也有兩種不同的收益率計算方法,第一種稱爲當期收益率,第二種稱爲到期收益率
下面我們主要分爲以下三種情況討論:(移動滑鼠檢視詳情)
- 平價債券
- 如果債券的價格等於其面值,那麼它的收益率等於債券的票面利率。
- 溢價債券
- 付息債券的價格高於面值
- 貼現債券
- 付息債券擁有低於面值的價格
到期收益率VS當期收益率
這裏,我們有兩種不同的收益率的計算方法,當期收益率適用於平價債券,而當面對溢價債券或貼現債券時,當期收益率便會忽視到期時債券價格發生變化的事實,因此,使用到期收益率來計算會更爲準確。
一年期的債券的收益率計算公式比較容易:
當期收益率=息票價值/價格
到期收益率=(息票價值+面值-價格)/價格
請看下面兩個具體的計算實例(移動滑鼠檢視詳情)
一年期的債券的收益率計算公式比較容易:
當期收益率=息票價值/價格
到期收益率=(息票價值+面值-價格)/價格
請看下面兩個具體的計算實例(移動滑鼠檢視詳情)
- 當期收益率
- 假設你擁有票面利率爲10%,面值爲1000美元的1年期附息債券,而它的市場價格現在是1047.62美元,
因此,其當期收益率=息票價值/價格=100/1047.62=9.55&。
- 假設你擁有票面利率爲10%,面值爲1000美元的1年期附息債券,而它的市場價格現在是1047.62美元,
- 到期收益率
- 假設你擁有票面利率爲10%,面值爲1000美元的1年期附息債券,而它的市場價格現在是1047.62美元,
因此,其到期收益率=(息票價值+面值-價格)/價格=(100+1000-1047.62)/1047.62=5%
- 假設你擁有票面利率爲10%,面值爲1000美元的1年期附息債券,而它的市場價格現在是1047.62美元,
- 結論
- 我們可以發現:
如果使用9.55%的當期收益率作爲假如購買該債券你所賺取收益率的指南,那麼你將被嚴重的誤導。
- 我們可以發現:
現實中更爲複雜的收益率
上一頁中,我們均假設附息債券的到期期限爲1年,而當期限超過1年時,計算其到期收益率的方法將更爲複雜
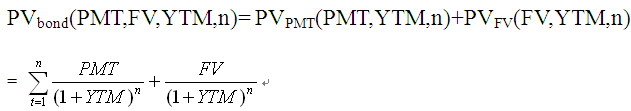
這裏n爲到期前每年支付的時期數量,YTM爲年到期收益率,PMT爲每年的息票支付,同時FV爲到期時得到的債券面值。
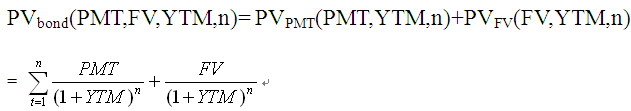
這裏n爲到期前每年支付的時期數量,YTM爲年到期收益率,PMT爲每年的息票支付,同時FV爲到期時得到的債券面值。
現實中更爲複雜的收益率
例:假設你考慮購買一隻票面利率爲10%的2年期附息債券,它的面值爲1000美元,同時,其當前價格爲1100美元,那麼該債券的收益率是多少?
當期收益率=100/1100=9.09%
到期收益率如下表:
由此我們可以得出一個一般原理:
溢價債券的到期收益率小於當期收益率,同時也小於票面利率
即:對於溢價債券而言:
到期收益率<當期收益率<票面利率
當期收益率=100/1100=9.09%
到期收益率如下表:
| n | i | PV | FV | PMT | 結果 |
|---|---|---|---|---|---|
| 2 | ? | -1100 | 1000 | 100 | i=4.65%=YTM |
由此我們可以得出一個一般原理:
溢價債券的到期收益率小於當期收益率,同時也小於票面利率
即:對於溢價債券而言:
到期收益率<當期收益率<票面利率
現實中更爲複雜的收益率
爲了便於大家更好的理解,我們來看另外一個例子
例:假設你考慮購買一隻票面利率爲4%的2年期附息債券,它的面值爲1000美元,同時,其當前價格爲950美元,那麼該債券的收益率是多少?
當期收益率=40/950=4.21%
到期收益率如下表:
由此我們可以得出另一個一般原理:
貼現債券的到期收益率大於當期收益率,同時也大於票面利率
即:對於貼現債券而言:
到期收益率>當期收益率>票面利率
例:假設你考慮購買一隻票面利率爲4%的2年期附息債券,它的面值爲1000美元,同時,其當前價格爲950美元,那麼該債券的收益率是多少?
當期收益率=40/950=4.21%
到期收益率如下表:
| n | i | PV | FV | PMT | 結果 |
|---|---|---|---|---|---|
| 2 | ? | -950 | 1000 | 40 | i=6.76%=YTM |
由此我們可以得出另一個一般原理:
貼現債券的到期收益率大於當期收益率,同時也大於票面利率
即:對於貼現債券而言:
到期收益率>當期收益率>票面利率
計算題
假設你擁有每年6%票面利率以及900美元價格的3年期債券(面值1000美元),那麼其當期收益率和到期收益率分別爲多少?
正確。
- 8.01%, 10.02%
- 6.67%, 8.01%
- 10.02%,8.01%
- 6.67%, 10.02%
影響收益率的因素
我們經常觀測到,具有相同到期期限的債券擁有不同的到期收益率,這是由於其收益率曲線不水準,到期收益率也將受到影響,有所不同。
下面我們來看,都有哪些因素將會影響收益率?(移動滑鼠檢視詳情)
下面我們來看,都有哪些因素將會影響收益率?(移動滑鼠檢視詳情)
- 票面利率的影響
- 當收益率曲線不是水準的時候,具有不同票面利率但到期期限相同的債券擁有不同的到期收益率。
- 違約風險與稅收的影響
- 無論違約風險多麼微小,一旦該債券招致某種違約風險,價格都會下降,同時,債券的收益率將會升高;
債券的納稅能力也會影響發行者或是債券類型的不同而發生變化。例如:美國州政府和地方政府發行的債券所賺取的利息是免徵聯邦所得稅的,這一特徵使得相對於其他類似債券,這些債券對繳納稅收的投資者更有吸引力,勢必將會導致債券價格升高,收益率更低。
- 無論違約風險多麼微小,一旦該債券招致某種違約風險,價格都會下降,同時,債券的收益率將會升高;
- 其他影響
- 可贖回型債券對發行者更具吸引力,因其有權在最終到期日之前贖回債券,因此將會降低債券的價格;
可轉換型債券對持有人更有吸引力,因其有權講債券轉換成預先確定數量的普通股票,因此將會抬高債券的價格。
- 可贖回型債券對發行者更具吸引力,因其有權在最終到期日之前贖回債券,因此將會降低債券的價格;
單選題
下列選項中,哪項可以用來衡量企業的違約風險?
正確
- 資產基礎
- 公司利潤
- 紅利史
- 公司信用評級
思考題
希臘債務危機愈演愈烈,使得全球金融市場發生動盪,並威脅到整個歐元區的經濟形勢。近日,希臘國債收益率大幅度提高,這顯示了市場認爲希臘債務違約風險增加,因而對其所持的希臘國債提出更高的收益要求。這就意味著希臘透過債券市場融資的成本在大幅度提高。這會進一步加重希臘政府的債務負擔。
希臘應該如何控制本國債券市場的穩定?歐盟的救援機制是否合理有效?希臘又是否能夠走出經濟頹勢?
參考資料:
希臘主權借貸成本升至創紀錄高點
希臘擬在美國發售數十億美元債券
把歐元一分爲二?
歐元區16國領導人就紓困希臘達成協議
希臘危機將損及根本
希臘應該如何控制本國債券市場的穩定?歐盟的救援機制是否合理有效?希臘又是否能夠走出經濟頹勢?
參考資料:
希臘主權借貸成本升至創紀錄高點
希臘擬在美國發售數十億美元債券
把歐元一分爲二?
歐元區16國領導人就紓困希臘達成協議
希臘危機將損及根本

小調查
爲改善數據訪問、提升質量並提高完整性,企業曾採取過什麼措施?(多選)
- 實施通用會計賬務系統
- 透過自動化和自助服務(如CFO門戶)梳順財務資訊的發送
- 運用系統性的數據清理和稽覈
- 建立非財務的數據標準(例如運營數據、人力資源(HR)數據)
- 從源頭進行電子數據採集(例如電子發票、光學字符識別技術、銷售點(POS))
- 採用第三方服務提供商提供的工具(例如工作流程工具、儀表盤)
總結
:
-
+
自動滾屏